AI智能体系统的架构设计与模式应用
1、常见工作流
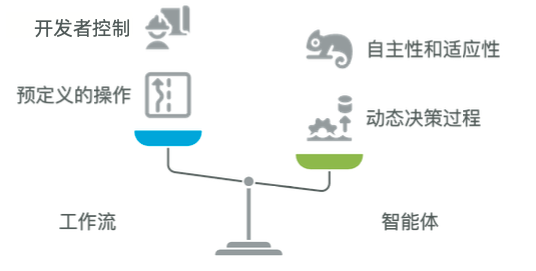
Anthropic 的研究突出了工作流(Workflow)和智能体(Agent)之间的一个关 键区别,即工作流指 LLM 和相关工具通过显式预定义的代码路径进行编排的系统。 这意味着操作序列、工具或 LLM 调用的条件以及整体任务执行流程都由开发者预先确定。相反,Anthropic 概念中的真正智能体具有更高程度的自主性。它们指的是由 LLM 动态指导自身流程的系统,能够实时决策工具的使用及实现目标所需的步骤。这类智能体始终掌控任务的执行过程,会根据输入和环境反馈调整方法,而非严格遵循预设路径。Anthropic 所识别和阐明的这些工作流模式,为在 LangGraph 中构建复杂的 AI 智能体系统提供了宝贵的框架。工作流和智能体之间的主要差异如图所示。
![image-20251130133200556]()